Blessed by the Potato

It’s been a long time since I’ve put up a weekly round-up post. It made sense to stop the practice: when I barely post once a week to begin with, all that would be left is round-up posts. For those visiting for the first time because of the inclusion in this week’s Carnival of Wealth, welcome! I wrote a welcome post not so long ago that still applies if you need to get oriented here.

First off, I submitted my last post on the cone of probability to the Carnival of Wealth, Dollars to Dollars Edition over at Control Your Cash. A quick note of correction: I have links to the past ~3 years of archived posts in the sidebar, but the WordPress archives actually go back about 9 years — I just truncated the sidebar because it was ridiculously long (and also anything before that point is really just whining about grad school and World of Warcraft and not really worth going back to).

Michael James is writing a book about retirement. Well, he hasn’t said he is in so many words, but he has been knocking out post after post examining how to safely turn an investment portfolio into spending money: Two posts on the 4% rule-of-thumb, and adjusting it for fees. A retirement income strategy of holding a certain portion in fixed income/cash and investing the rest, with follow-ups on this cushioned strategy. Revisiting that strategy he works out some example cases with a smoothing filter on adjusting spending to market returns, and some historical perspective. Finally, some thoughts on treating your whole portfolio like a RRIF.

Sandi gets a post up at Spring just in time for inclusion, talking about budgeting as the most important aspect of personal finance (even though it sucks).

I don’t read many parenting blogs, but recently came across Illustrated with Crappy Pictures and she’s hilarious. If you have to start somewhere in the archives, you might as well with this post: “Parties without cookies are not really parties at all. They are just groups of people feeling disappointed.”

[Update: this post appears in the Carnival of Wealth, Dollars to Dollars Edition]

Here is how many people plan for retirement (and many similar activities that involve projections): come up with reasonable estimates of the relevant parameters. Plug it into an online calculator or spreadsheet to do the math. Have a cookie.

Yet you really can’t just say that the average investment return is 6%, your average spending needs are $40k/yr and inflation will hit 2%, plug that into a spreadsheet, and call your financial planning exercise completed. That might be your expected, most likely outcome and an excellent start. You can plot it for a nice, smooth exponential growth trajectory like this:

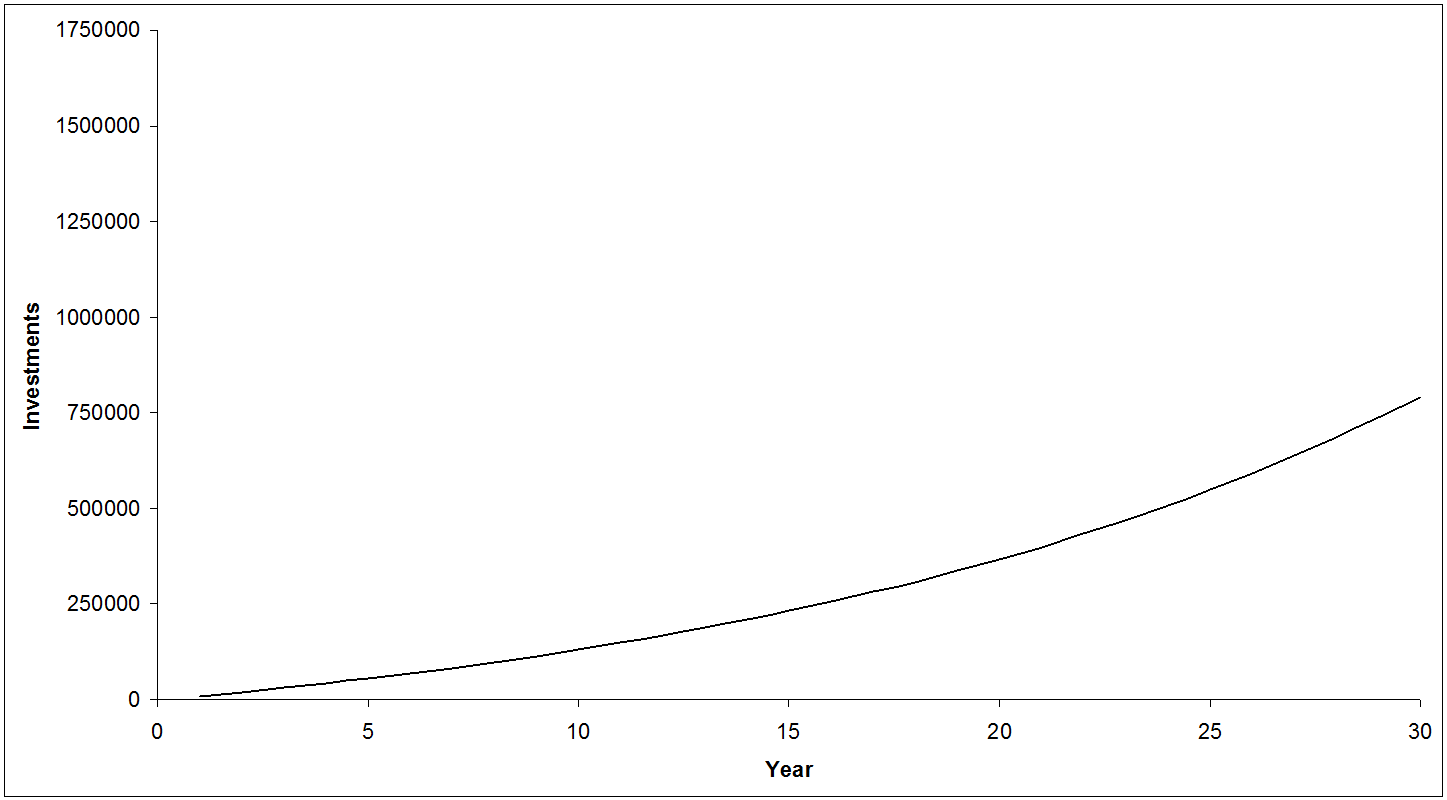
A very comforting graph: continually saving money, making steady returns, you move smoothly towards your retirement goal. While your future might have a good chance of looking something like that, it’s highly unlikely to be precisely like that. There’s a whole range of possible outcomes. So we don’t want to just plot the course that’s going to get us there. Take a few minutes and add a “95%¹ best case” and “95% worst case” projection. How would those scenarios affect your plans?

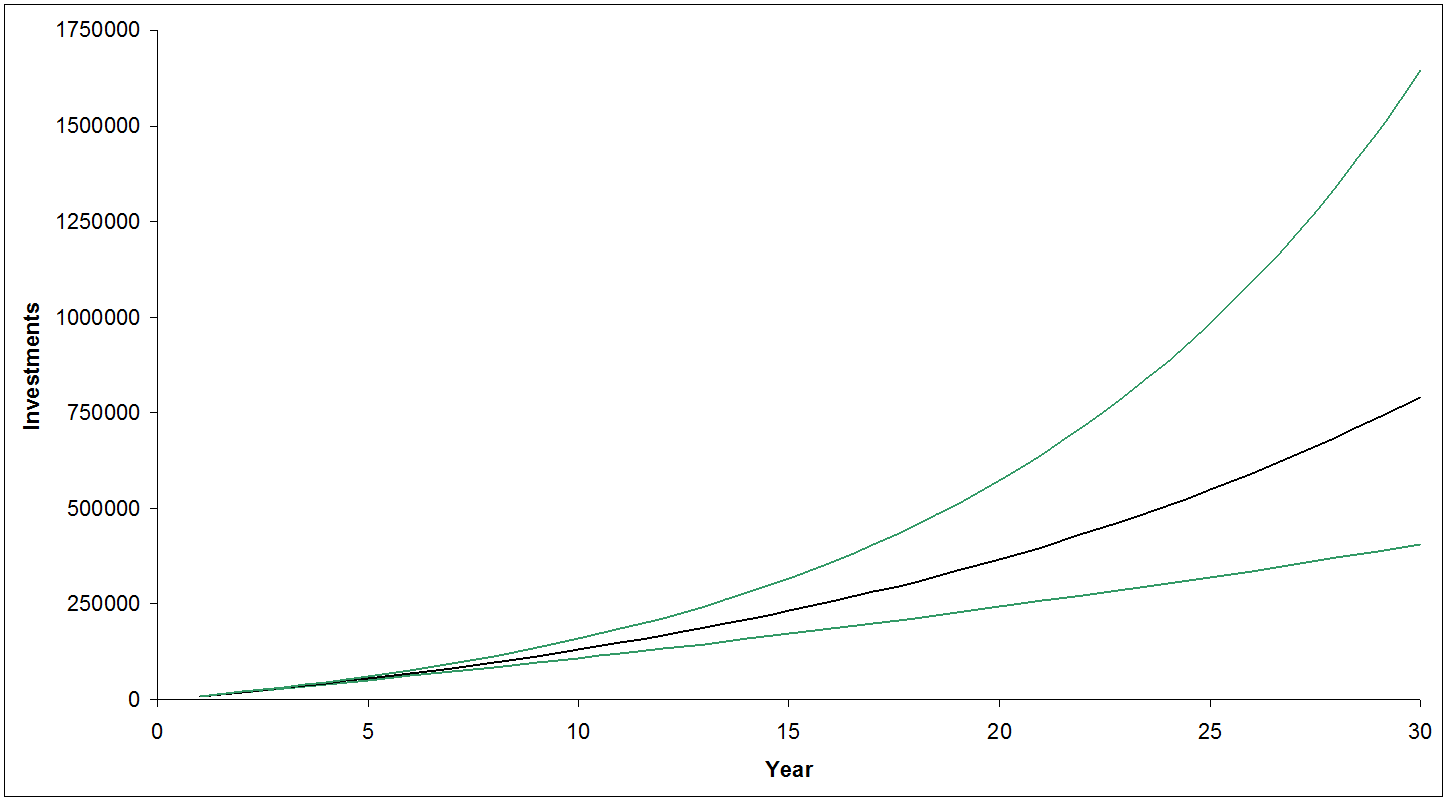
That’s a fair bit better: you have some idea of the range of future outcomes, and may even be able to say how those might compare to what you’re willing to accept, and set some limits and guidelines for your future course corrections. Maybe if by year 5 you’re closer to the bottom line than the middle one, you’ll increase your savings rate to compensate. But even that is not really capturing the uncertainty and more importantly the variability ahead. There’s a big cloud of probability around the outcomes, and this is just a small, simplified part of a projection to retirement.

Maybe describing it as a cone of probability is a better way of putting it. This helps visualize all the uncertainty that we face going into the future. Note that I made the bottom edge creep up over time; this works with some recent posts by Michael James about stocks becoming less risky over time. Next year the market could be down 50% in a repeat of 2008, but 30 years from now it’s very likely that the market will be up. Up less than your projected 6% real return perhaps, which could be a challenge to your initial plan, but up nonetheless.

Because the future is so inherently uncertain, I generally tell people with a lot of future ahead of them to not sweat the fine details: tweaking your asset allocation to the last half a percent really won’t matter when you can only guess at future returns to plus or minus 5% CAGR over 30 years. Control what you can (keep fees low, save some decent amount of your income, start early, don’t panic), and be prepared to be surprised and make adjustments. Get started in approximately the right direction, try to keep moving in the right direction through an iterative process, and try not to fear the uncertainty. Uncertainty is a fact of life. The future will — at best — only look approximately like how we imagine it will.

That’s a tough, uncomfortable concept for many. We demand rigidly defined areas of doubt and uncertainty! The unknown is scary and foreign and weird, and people just don’t like the unknown; uncertainty looks a lot like that with some kind of math mixed in (which is frightening and uncomfortable in its own right). As terrifying as this is going to sound: you can’t hide from uncertainty. That’s just the nature of life (and if it was less uncertain it would be boring).

A plan that includes a big cone of probability and uncertainty may actually be more useful than one that pretends there is no uncertainty in the future, though the single line, ever-upwards trajectory was a lot more appealing to our baser selves.

Podcast podcast podcast! In case you missed it, we talked about these issues (and I unveiled these terrible excel/photoshop hybrids) in the because money podcast earlier in January.

Footnote: pardon me for using photoshop to make the probability clouds. I should have used MATlab or something with an actual Monte Carlo simulation, but I don’t actually have it on any of my current computers — I’d have to go fire up my ancient Pentium 3 system as it’s the only one left in the house that still has MATlab and Maple. The consequence is that the clouds are not particularly accurate, and aren’t as much like cones as I would have liked. Hopefully the visual still works for you.

1 – By which I mean in a stats sense your 95% confidence interval — or in a more plain language sense — aside from a few extreme cases, the range your results will most likely fall within.

“I got the flu shot but got sick anyway!”

I’ve heard that line so many times. Without running off on too long a rant, people call any bad cold “the flu”, but I haven’t heard of anyone who said “I had a laboratory-confirmed diagnosis of influenza A or H1N1 even though I got the shot!” The flu shot will protect you from a few strains of the flu for that year. You can still catch a cold, or strep throat, or a bacterial sinus infection — or even a less-common form of influenza that wasn’t included in the shot. Indeed, I’m sitting here with a nasty cold even though I got the flu shot. Fortunately, I’m currently participating in a study that seeks to test these types of claims, so I should know in a few weeks what the results from my nasal swab are, and whether I actually have the flu or some other nasty virus. Right now in Toronto, about a quarter of monitoring nasal swabs are coming back positive for influenza; I don’t know how many of those people had the shot, but it makes for a lot of sick people who really just have colds.

I heard of a very clever, tongue-in-cheek test to see whether you have actual influenza or just a seasonal cold called “the fifty-dollar test.” Simply go to a sick person’s bed, and put some money at the foot of it. If they say “fuck it, I am too sick to reach down to the foot of the bed and get that money” for anything under a $50, they have the flu. If a $20 bill will motivate you to move your stuffy, feverish head and aching body enough to grab that free money, you just have a cold.

This year’s flu season seems a bit worse than usual, with H1N1 reappearing and striking the young and otherwise healthy people who usually skip through flu season. Many people are now (belatedly) rushing for their flu shots, leading to supply issues. If getting vaccinated at these higher rates becomes more habitual for the years to come, that’s going to help increase herd immunity and make the average future flu seasons less severe.

As our regular flu season becomes tamer, with more people vaccinated and fewer people infected each year, we might be at an increased risk of hearing “I got the flu shot but got sick anyway!” Because of course we could have one bad year where the scientists determining which strains to include in the vaccine miss a big one, and it runs through the population.